Problem Statement

Determine if a sudoku is Valid.

Solution Explanation

Given a sudoku grid, we need to verify if the already filled in numbers doesn't violate the sudoku rules. The rules are very simple,

• Each row has numbers from 1-9 and no repitions
• Each column has numbers from 1-9 and no repitions
• Each 33 cube has numbers from 1-9

For example, given the below sudoku,

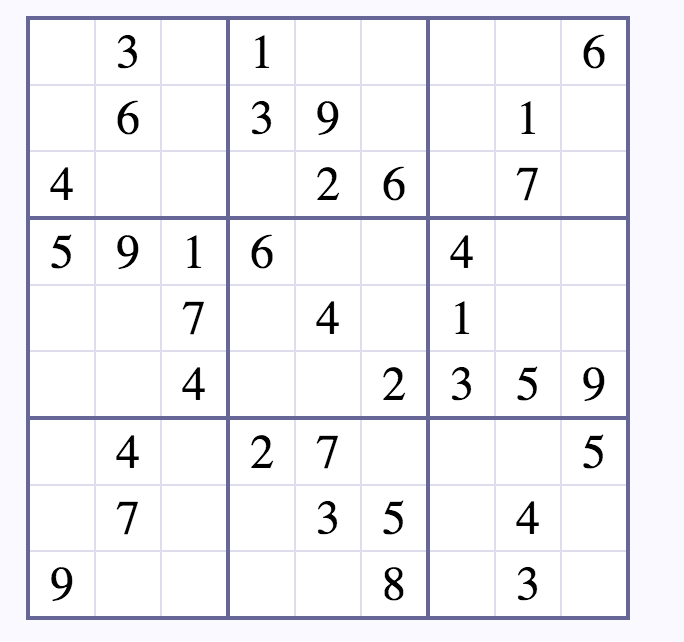
There are no rows or columns or 3*3 grid which violate the above rules.For validating the grid, we could use the following psuedocode:

    for i=0 to rowlen-1
        declare rowset, colset, cubeset
        for j=0 to collen-1
            check if the grid[i][j] is in a row set, if yes, return false
                  else add to row set
            check if the grid[j][i] is in a col set, if yes, return false
                  else add to col set
            check if the neighbor cell in the grid is not present in cubeset,
            if yes, return false
                   else add it to cube set
    

We can do all this while traversing through the grid only once and below is the complete java implementation,

class ValidateSudoku {
    public boolean isSudokuValid(char[][] board) {
		if (board == null || board.length == 0)
			return true;
		int rowlen = board.length, collen = board[0].length;
		for(int i=0;i<rowlen;i++){
			Set<Character> rowSet = new HashSet<>();
			Set<Character> colSet = new HashSet<>();
			Set<Character> gridSet = new HashSet<>();
			for(int j=0;j<collen;j++){
				if(board[i][j]!='.' && !rowSet.add(board[i][j]))
					return false;
				if(board[j][i]!='.' && !colSet.add(board[j][i]))
					return false;
				    int RowIndex = 3*(i/3);
		            int ColIndex = 3*(i%3);
		            if(board[RowIndex + j/3][ColIndex + j%3]!='.' && !gridSet.add(board[RowIndex + j/3][ColIndex + j%3]))
		                return false;
			}
		}
		
		return true;
	
    }
}

Time Complexity

Since we traverse through the grid only once, the time complexity is O(n^2).